

스택오버플로우에서 찾은 내용을 기반으로 신경망에서 편향의 역할을 정리해봤습니다.
출처 - https://stackoverflow.com/questions/2480650/what-is-the-role-of-the-bias-in-neural-networks
2022. 3. 9 - 최초작성
먼저 편향이 없는 입력과 출력이 하나인 신경망을 고려해봅니다.

입력 x에 가중치 w0을 곱한 결과를 활성화 함수의 입력으로 사용합니다. 활성화 함수의 성질에 따라 결정되는 출력이 신경망의 출력이 됩니다.
여기에선 활성화함수로 시그모이드(sigmoid) 함수를 사용합니다.
y = sigmoid(x * w0)
아래 그림은 가중치 w0 값을 변화시키며 입력 x 에 대한 신경망의 출력 y를 보여줍니다. 활성화 함수로 시그모이드를 사용했기 때문에 형태가 시그모이드 모양입니다.
가중치 w0를 변경하면 시그모이드 활성화 함수의 중앙에 보이는 곡선의 가파른 정도가(steepness) 변경됩니다.

지금 상황에서는 입력(x)이 2일 때 신경망에서 0을 출력하게 하는 것이 불가능합니다. 시그모이드 함수의 가중치(w0)이 변하더라도 곡선의 중심은 x=0을 벗어나지 못하기 때문입니다. 원하는 결과를 얻으려면 곡선을 오른쪽으로 이동해야 합니다.
이것이 편향(bias)가 필요한 이유입니다.
편향(bias)를 추가하면 이제 신경망의 출력은 sigmoid(w0*x + w1*1.0)가 됩니다. 편향 뉴런의 값이 1인 이유는 다른 영향을 주지 않고 편향 뉴런과 출력 뉴런 사이 연결에 부여되는 편향 가중치(w1)을 출력 뉴런에 전달하기 위해서입니다.

가중치(w0)이 고정된 상태에서 편향 가중치 (w1) 값을 변화시키며 얻은 네트워크의 출력은 다음과 같습니다.
y = sigmoid(w0 * x + w1 * 1.0) = sigmoid(w0 * x + w1)

이제 편향 가중치 w1이 -5가 되면 곡선이 오른쪽으로 이동하므로 x가 2일 때 0을 출력하는 신경망이 됩니다.
편향은 직선의 방정식에서 y절편 b로 생각할 수 있습니다.
아래 그림에서 노란색으로 표시된 각 점을 설명하는 하나의 직선 사이의 전역 오류를 최소화하려면 적절한 기울기와 y절편을 갖는 함수를 구해야 합니다.
y = ax + b
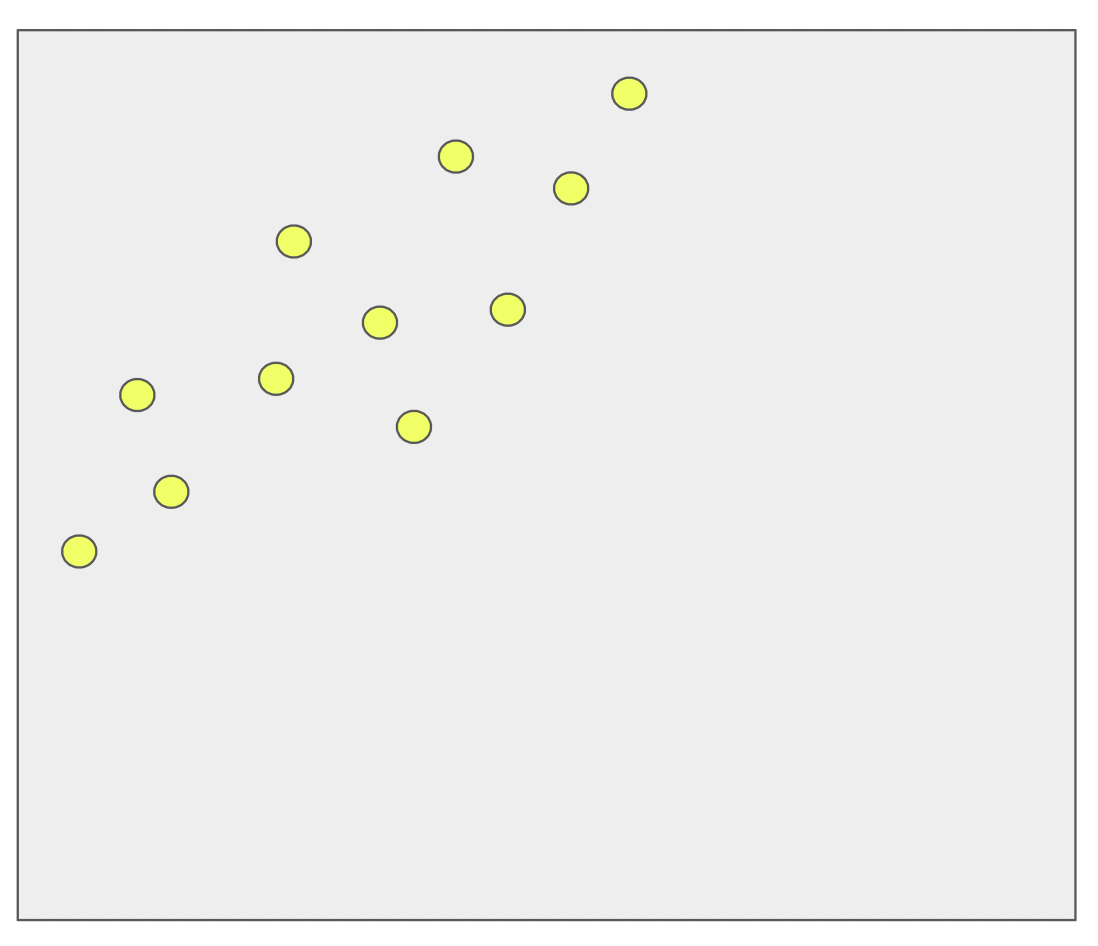
만약 편향 b가 없으면 직선 y = ax 는 항상 원점(0, 0)을 통과하므로 아무리 최적의 파라미터를 구하더라도 모델의 예측은 데이터를 만족스러울 정도로 맞추기(fit)가 힘들어집니다.
2차원 평면에 점들이 흩어져 있고 이를 잘 설명하는 하나의 함수 y = ax + b를 찾는 경우를 상상해보세요.
아래 그림처럼 편향 b가 없으면 직선 y = ax는 원점을 항상 통과하므로 노란점으로 표시된 데이터를 제대로 나타내지 못합니다.

y절편 b를 추가하면 편향을 조정하여 모델의 예측을 데이터와 더 잘 맞추기 위해 직선을 위아래로 이동할 수 있습니다.
y = ax + b
아래 그림처럼 직선이 원점을 통과하지 않아도 되기때문에 좀더 데이터를 더 잘 나타낼 수 있게 됩니다.

아래 이미지들은 2변수 회귀 문제에서 편향 뉴런이 있거나 없는 경우 간단한 2층 피드포워드 신경망의 결과를 보여줍니다.
편향(bias)이 없으면 ReLU를 활성화함수로 사용한 신경망은 (0,0,0)에서 벗어날 수 없습니다.



다음 코드를 사용하여 그래프를 그렸다고 합니다.
https://github.com/JaPhi/NN_autograd_bias/blob/main/NN_autograd_bias.py
'Deep Learning & Machine Learning > 딥러닝&머신러닝 개념' 카테고리의 다른 글
| LoRA( Low-Rank Adaptation of Large Language Models ) 개념 간단 정리 (1) | 2024.02.22 |
|---|---|
| 기대값이란 (0) | 2023.11.05 |
| 정규화(Normalization), 표준화(standardization), 이상치(outlier) 제거 (0) | 2023.10.23 |
| XGBoost 개념 정리 (0) | 2023.10.18 |
| 난수 생성에서 시드(seed) 사용하는 이유 (0) | 2023.10.12 |




