

LoRA 개념을 간단히 간단히 정리했습니다.
2024. 2. 4 최초작성
2024. 2. 8 그림 추가
2024. 2. 22 내용 보충
대규모 언어 모델(LLM)은 방대한 양의 데이터 세트에 대한 광범위한 학습을 진행합니다. 하지만 이렇게 학습된 지식은 일반화된 지식이어서 높은 정확도가 요구되는 특정 분야의 작업에는 충분하지 않을 수 있습니다.
다행인 것은 특정 분야의 작업을 위해 학습시킬때 처음부터 할 필요가 없습니다. 미세 조정(파인 튜닝)을 통해 기존의 학습된 가중치를 조정함으로써 모델을 특정 작업에 맞게 최적화할 수 있습니다. 하지만 모델이 큰 경우엔 노트북에서 사용되는 GPU에서는 미세 조정이 어려운 작업입니다. 이것을 가능하게 해주는 것이 LoRA입니다.
LoRA의 핵심 아이디어는 모델의 가중치를 직접 수정하는 대신, 가중치 변화를 효율적으로 모델링하기 위해 행렬 분해 기법을 사용한다는 데 있습니다. 이 접근 방식에서 "내재적 순위(intrinsic rank)"가 낮다는 가설은 행렬을 둘로 나누어 계산하는 것과 직접적인 관련이 있습니다. 구체적으로, 원래의 가중치 행렬을 수정하는 대신, 가중치 변화를 나타내는 데 필요한 정보를 포함하는 더 작은 두 행렬로 분해합니다. 이렇게 함으로써, 전체 가중치 행렬을 직접 조정하는 것보다 계산 효율성이 향상됩니다.
가중치 변화가 낮은 내재적 순위를 가진다는 것은 전체 가중치 행렬을 직접 수정하는 대신, 더 작은 차원의 행렬을 사용해도 모델 적응에 필요한 주요 변화를 충분히 표현할 수 있다는 의미입니다. 이 두 행렬은 원래 가중치 행렬에 적용되어, 변화를 모델에 통합합니다. 이 방법은 모델의 성능을 유지하면서도 파라미터의 수를 적게 늘리고, 계산 비용을 절감할 수 있게 해줍니다. LoRA를 사용함으로써, 미세 조정 과정에서 필요한 메모리와 계산 자원을 크게 줄일 수 있으며, 이는 특히 큰 모델을 소규모 하드웨어에서 효율적으로 미세 조정하려는 경우에 유용합니다.
모델이 점점 더 커짐에 따라 모든 파라미터를 직접 파인 튜닝하려면 상당한 비용과 시간이 발생합니다. 따라서 최근 몇 년 동안 파라미터를 효율적 파인 튜닝(PEFT)하는 연구가 진행되고 있습니다. PEFT 중 하나인 LoRA를 사용하면 사전 학습된 모델의 가중치를 동결하고 작은 모델로 파인 튜닝하여 뛰어난 파인 튜닝 결과를 얻을 수 있습니다.
LoRA(Low-Rank Adaptation of Large Language Models)는 학습할 파라미터의 개수를 크게 줄여주는 학습 기법입니다. 이 기법은 기존 모델에 있는 가중치는 그대로 두고 모델에 기존보다 적은 수의 새로운 가중치를 삽입하고 새로 추가한 가중치만 학습하는 방식으로 동작합니다. 따라서 LoRA를 사용하면 더 적은 메모리를 사용하여 훨씬 빠르게 학습이 가능하며 더 작은 모델 가중치(수백 MB)를 생성하기 때문에 저장 및 공유하기가 더 쉽습니다.
대규모 신경망 모델의 파라미터를 파인 튜닝(fine-tuning)하는 대신, 더 작은 모델이나 가중치를 훈련하고 이를 원래 LLM의 특정 레이어 가중치와 결합할 수 있습니다. GPT-3 모델을 파인 튜닝하는 것과 비교하면 LoRA는 훈련 파라미터가 10,000배 더 적고 GPU 사용량은 1/3에 불과합니다.
LoRA( Low-Rank Adaptation of Large Language Models )에 있는 Low Rank의 의미를 알아보기 위해 몇까지 관련 개념을 살펴봅니다.
행렬의 랭크(rank )
행렬의 랭크는 행렬의 열 또는 행 중에 다른 행 또는 열의 정수배가 아닌 즉 선형독립인 행 또는 열의 최대 개수입니다. 선형 독립이라는 것은 어떤 벡터가 다른 벡터들의 선형 조합으로 표현될 수 없다는 것을 의미합니다. 예를 들어, 행렬 A의 Rank가 r이라면, 이 행렬은 r개의 선형 독립인 행 벡터 또는 열 벡터를 가지고 있다는 의미입니다.
Full Rank 행렬
행렬이 가능한 최대 랭크를 갖는 경우를 말합니다. 이는 행렬의 행 전체 또는 열 전체가 선형 독립인 경우에 해당합니다.
예를 들어, m x n 크기의 행렬에서( m은 행렬의 행수, n은 행렬의 열수입니다.)
만약 행렬이 행 전체 랭크(full row rank)를 갖는다면, 이는 행렬의 모든 행 벡터들이 선형 독립임을 의미하며, 이 경우 행렬의 랭크는 m입니다 (여기서 m은 행렬의 행 수).
만약 행렬이 열 전체 랭크(full column rank)를 갖는다면, 이는 행렬의 모든 열 벡터들이 선형 독립임을 의미하며, 이 경우 행렬의 랭크는 n입니다 (여기서 n은 행렬의 열 수).
행렬이 전체 랭크(full rank)를 갖는다고 할 때, 이는 행렬이 정방행렬(square matrix, 즉 (m = n))일 경우에 해당하며, 모든 행과 열이 선형 독립인 경우를 의미합니다. 전체 랭크를 갖는 행렬은 역행렬을 가지며, 따라서 가역(invertible) 또는 비특이(non-singular)라고 불립니다.
Low-Rank 행렬
Low-Rank 행렬은 행렬의 Rank가 행렬의 행 수나 열 수보다 작은 경우를 말합니다. 즉, 행렬의 모든 정보나 구조가 상대적으로 적은 수의 행 또는 열 벡터들에 의해 완전히 표현될 수 있는 경우입니다.
Low-Rank 행렬은 종종 두 개 또는 그 이상의 더 작은 행렬의 곱으로 분해될 수 있습니다. 예를 들어, m x n 행렬 A가 Rank r인 경우, A는 m x r 행렬과 r x n 행렬의 곱으로 표현될 수 있습니다.
행렬 분해(Matrix Factorization)
복잡한 행렬을 더 간단하거나 해석하기 쉬운 여러 행렬의 곱으로 나타내는 과정을 의미합니다. 이 방법은 데이터의 숨겨진 특징을 발견하고, 차원을 축소하며, 데이터를 압축하는 데 유용하게 사용됩니다.
Pre-training (사전 학습)
사전 학습은 모델을 특정 작업에 적용하기 전에, 대규모의 일반적인 데이터셋을 사용하여 모델의 가중치를 초기화하거나 학습시키는 과정입니다. 이 단계에서 모델은 광범위한 지식을 습득하며, 이를 기반으로 특정 작업에 더 효과적으로 적응할 수 있습니다. 이 과정은 특히 데이터가 부족한 작업에서 유용하며, 모델이 보다 복잡한 패턴을 인식하고 일반화할 수 있도록 돕습니다. 사전 학습된 모델은 다양한 작업에 재사용될 수 있으며, 작업 특화 데이터만을 사용하여 학습하는 것보다 더 빠르게 좋은 성능에 도달할 수 있습니다.
Fine-tuning (파인 튜닝)
파인 튜닝은 사전 학습된 모델을 사용하여 특정 작업이나 데이터셋에 맞게 모델의 가중치를 미세 조정(파인튜닝)하는 과정입니다. 이 단계에서는 작업 특화 데이터셋을 사용하여, 모델이 특정 작업에 더 잘 적응하도록 학습시킵니다. 사전 학습된 모델에 비해 작은 데이터셋으로도 효과적인 학습이 가능합니다.
LLM 모델인 Llama-70B을 파인 튜닝하면 70B개(700억개)의 파라미터를 업데이트하게 됩니다. 이 작업은 매우 오래 걸리며 컴퓨팅 리소스를 많이 필요합니다.
LoRA를 이해하려면 행렬의 랭크(rank)와 행렬분해(decomposition)에 대한 개념을 이해하는 것이 중요합니다. 간단히 말해, 행렬의 랭크는 선형적으로 독립적인 행 또는 열의 개수입니다. 즉 다른 행이나 열에 정수를 곱해서 만들 수 없는 고유한 행 또는 열의 개수입니다.
다음과 같은 2 x 3 크기의 행렬 X가 있다고 할때

두 번째 행이 첫 번째 행의 세 배라는 것을 알 수 있는데, 이는 행렬 X에 고유 행이 하나만 있으므로 랭크 1 행렬이 된다는 것을 의미합니다. 따라서 행렬 X는 아래처럼 두 개의 작은 행렬인 A 와 B로 각각 크기가 2×1과 1×3인 두 개의 작은 행렬로 분해할 수 있습니다

이제 full-rank 행렬 X 대신 두 개의 low-rank 행렬 A와 B로 표현할 수 있습니다.
가중치 행렬 W∈R^ 1000×100은 두개의 낮은 차원의 행렬 B∈R^1000×10과 A∈R^10×1000으로 분해하여 원본 가중치 행렬을 low-rank 근사화할 수 있습니다. W ≈ BA로 표현될 수 있으며 여기서 BA는 원래 가중치 행렬 W와 같은 차원을 가지지만 더 낮은 랭크를 가집니다. 식으로 나타내면 다음과 같습니다.

여기서 h는 현재 레이어의 출력, W_0은 사전 학습된 원래 가중치로 학습중 고정되며, ΔW는 원래 가중치에 추가되는 가중치로 학습중 업데이트됩니다. BA는low-rank 가중치, x는 입력입니다.
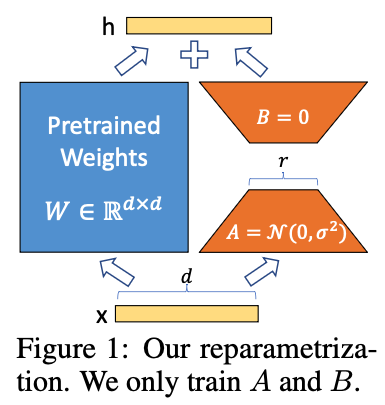
위 그림에서 입력 X∈R^d 가 주어졌을 때 왼쪽 파란색 부분은 원래의 사전 학습된 가중치 W∈R^d×d 를 나타내며, 오른쪽 주황색 부분은 두 개의 낮은 순위 행렬 A∈R^d×r와 B∈R^r×d 를 나타냅니다. 추론하는 동안 원래의 가중치와 행렬 BA를 추가하여 이전 방정식에서 설명한 대로 출력 h를 얻을 수 있습니다. 참고: A에는 무작위 가우시안 초기화를 사용하고 B에는 0을 사용하므로 훈련 시작 시 ∆W = BA는 0입니다.
Lora
파인 튜닝은 사전학습된 모델을 다른 테스크의 데이터셋으로 학습하기 위해 기존 사전학습된 모델의 모든 가중치를 업데이트해야 합니다. 따라서 파인 튜닝을 하기 위해 상당히 오랜 시간과 많은 컴퓨팅 리소스가 필요하게 됩니다.
LoRA는 사전 학습된 모델의 기존 가중치는 그냥 두고 새로운 가중치만 학습시키는 방법입니다. 따라서 학습하는데 걸리는 시간과 컴퓨팅 리소스가 줄어들게 됩니다.
예를 들어 Llama-70B 모델이 70B(700억개 파라미터)의 가중치를 갖는 N x M 크기의 가중치 행렬을 가진다고 가정합시다. N과 M보다 작은 수 K를 선택하여 N x K와 K x M 크기를 갖는 새로운 가중치 행렬 UA와 UB을 생성합니다. UA x UB는 N x M과 똑같은 크기의 행렬을 생성하지만 UA와 UB 행렬에 저장된 파라미터 개수는 줄어들게 됩니다. K는 튜닝해야 하는 하이퍼파라미터로, K가 작을수록 LLM 모델의 성능이 떨어집니다.
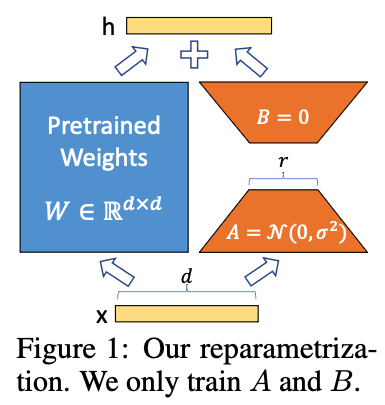
이제 70B 모델의 N x M 가중치 행렬 W(위 그림에서 파란색)를 업데이트하는 대신 UA x UB 가중치 행렬 ΔW(위 그림에서 주황색)를 업데이트합니다.
Y = m x W + B 방정식에서 가중치 W와 바이어스 B는 튜닝이 되지 않는 값입니다.
모델을 학습시키면 W는 업데이트된 가중치 Wu가 됩니다. 여기서 Wu는 W+ΔW를 의미합니다. ΔW는 기본 가중치 W에 대한 업데이트된 가중치입니다.
Y = m x Wu + B = m(W+ΔW) + B = m(W+UA x UB) + B
W를 학습시키는 대신 ΔW 즉, UA x UB만 학습시킨 후, W에 더해줍니다. 이것이 LoRA의 작동 방식에 대한 전체적인 아이디어입니다. 아이디어는 간단하지만 이점은 매우 큽니다.
예를 들어, Llama 70B 모델은 가중치가 700000 x 100000 행렬을 갖는데 랭크가 10이라면 가중치는 700000 x10 크기와 10 x 100000 크기의 행렬인 UA와 UB로 분해됩니다.
파인 튜닝을 할 경우엔 전체 파라미터인 70B(700000 x 100000 = 700억개)를 업데이트하는 반면 LoRA를 사용하면 UA와 UB의 크기인 700만개(=700000 x10)와 100만개(=10 x 100000)만 업데이트하면 됩니다. 즉 기존 700억개보다 적은 8백만 개의 파라미터만 업데이트하면 되므로 파리미터의 개수가 약 98.86% 감소하여 계산하는데 걸리는 시간이 줄어들게 됩니다.
다시 적어보면, 행렬 W∈R^d×k 의 경우, 이를 두 개의 행렬 B∈R^d×r 과 A∈R^r×k 로 분해할 수 있으며, 여기서 r ≫ min(d,k) 입니다.
LoRA는 계산 시간과 훈련 시간을 절약할 뿐만 아니라 파괴적 망각(catastrophic forgetting)을 방지하는 데도 도움이 됩니다.
파괴적 망각이란 간단히 말해 신경망 같은 머신 러닝 모델이 이전에 학습한 작업 수행 방법을 잊어버리는 것으로, 특히 사전 학습된 모델에 대한 파인튜닝을 통해 새롭고 다른 작업을 학습할 때 발생합니다. 새로운 작업을 학습하면서 전체 파라미터를 조정하기 때문에 이전에 배웠던 작업을 까먹게 됩니다.
LoRA는 파괴적 망각을 방지합니다. 사전 학습된 가중치를 업데이트하지 않고 새로 만든 가중치만 업데이트하기 때문에 모델은 이미 학습한 내용을 절대 잊지 않습니다. 일반적인 파인튜닝에서는 전체 가중치를 업데이트하기 때문에 치명적인 망각이 발생할 가능성이 있습니다.
LoRA의 장점
원본 가중치 행렬에 대한 업데이트가 수행되지 않으므로 low-rank 가중치 행렬의 가중치만 저장하면 됩니다. 필요시 원래 가중치 행렬에 low-rank 가중치 행렬을 더해서 사용하면 됩니다.
원본 가중치 행렬에 대한 여러 가지 작업을 할 경우 각각 원본 가중치 행렬로 저장하지 않고 각각에 대한 low-rank 가중치 행렬만저장했다가 필요시 원본 가중치 행렬에 더해서 사용하는 방식을 취하면 저장공간을 절약할 수 있습니다.
QLoRA란 무엇인가요?
QLoRA에서 Q는 양자화를 의미합니다. 즉 가중치의 수치 표현의 정밀도를 낮추는 과정을 의미합니다. 그 결과 LoRA 방식에 비해 학습에 필요한 메모리 크기를 줄여줍니다.
신경망은 보통 32비트 또는 64비트의 부동 소수점 숫자를 사용하여 가중치를 나타냅니다. 그러나 이러한 고정밀 표현은 특히 모바일 디바이스나 엣지 디바이스와 같이 리소스가 제한된 하드웨어에서는 계산 비용이 많이 들 수 있습니다. 그래서 대신 실수 16비트나 정수 8비트 처럼 낮은 정밀도의 데이터 유형을 사용하면 모델 크기를 줄이고 계산 리소스를 크게 절약할 수 있습니다.
QLoRA는 기본적으로 양자화된 LLM, 즉 메모리에 더 낮은 정밀도의 데이터 유형을 사용하여 로드된 LLM에 대한 LoRA입니다.
QLoRA를 사용하면 정보 손실이 발생하므로 성능에 약간의 영향을 미칠 수 있습니다.
논문
LoRA: Low-Rank Adaptation of Large Language Models, ICLR 2021.
https://arxiv.org/abs/2106.09685
참고
https://huggingface.co/docs/diffusers/main/en/training/lora
https://jacksoncakes.com/2023/10/01/road-to-efficient-llms-1-lora/
'Deep Learning & Machine Learning > 딥러닝&머신러닝 개념' 카테고리의 다른 글
| 모델 평가하는 방법(혼동행렬, confusion matrix 사용방법, 특이도, 민감도, 재현율, 정확도, 정밀도) (0) | 2024.06.03 |
|---|---|
| Fine-tuning 개념 (0) | 2024.03.02 |
| 기대값이란 (0) | 2023.11.05 |
| 신경망(neural networks)에서 편향(bais)의 역할 (0) | 2023.10.28 |
| 정규화(Normalization), 표준화(standardization), 이상치(outlier) 제거 (0) | 2023.10.23 |



