

분산과 표준 편차 차이를 정리했습니다. 오류가 있을 수 있습니다.
2022. 02. 06 최초작성
어떤 하나의 통계적 관찰 대상이 되는 집단전체를 모집단이라 하고, 그 부분집단을 표본이라고 한다.
https://ko.wikipedia.org/wiki/모집단
분산을 구할때 모집단과 표본(sample) 중 어느 쪽을 대상으로 하느냐에 따라 계산 방법에 차이가 있습니다. 우선은 집단 전체를 의미하는 모집단이라고 가정하고 진행한 후, 포스트 마지막에서 모집단의 부분집단인 표본(sample)인 경우에 달라지는 부분을 설명합니다.
모집단 또는 표본에 포함된 대상을 원소라고 하겠습니다. 원소 대신 샘플이라고 사용하는 경우가 있는데 이러면 표본(sample)과 혼동이 될 우려가 있기 때문입니다.
분산(Variance)
분산은 각 원소에서 평균을 빼서 제곱한 것의 평균을 구한 것입니다.
다음처럼 분산을 계산합니다.
1. 전체 원소에 대한 평균을 구합니다.
2. 각 원소에서 평균을 뺀 후, 제곱합니다.
3. 2번에서 구한 값들의 모두 더한 후, 원소 개수로 나눕니다.
표준 편차(Standard Deviation)
표준 편차는 원소들이 평균으로 부터 얼마나 퍼져 있는지 측정합니다.( 원소들이 평균 근처에 모여있지않고 얼마나 멀리 떨어져있는지를 의미합니다.)
기호로 그리스 문자 σ(시그마)를 사용합니다.
표준편차는 분산의 제곱근으로 구합니다.
분산과 표준편차를 구하는 식은 다음과 같습니다.
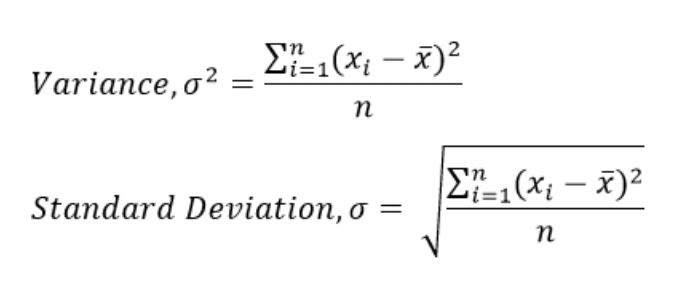
정규 분포
정규 분포(normal distribution) 또는 가우스 분포(Gaussian distribution)는 연속 확률 분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는 데에 자주 사용되며, 이것은 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다.
정규분포는 2개의 매개 변수 평균 𝜇과 표준편차 𝜎에 대해 모양이 결정되고, 이때의 분포를 N(𝜇, 𝜎2)로 표기한다. 특히, 평균이 0이고 표준편차가 1인 정규분포 N(0, 1)을 표준 정규 분포(standard normal distribution)라고 한다.
https://ko.wikipedia.org/wiki/정규_분포
모집단에서 추출할 때마다 표본을 구성하는 원소들은 달라지므로 표본의 평균도 변화합니다. 중심극한정리는 이러한 표본평균의 분포가, 표본의 크기가 충분히 클 경우, 정규분포에 접근한다는 것을 의미합니다. 따라서 표본의 원소 개수가 많을수록 그 분포는 정규분포에 더 가까워집니다.
https://blog.naver.com/mykepzzang/220851280035
https://blog.naver.com/owl6615/221847019934
분산은 샘플에서 사용한 단위의 제곱을 사용하지만 표준 편차는 샘플에서 사용하는 단위를 사용합니다.
예를 들어 평균 10, 표준편차 3인 정규 분포(Normal distribution)와 평균 10, 분산 9인 정규분포는 똑같습니다.
표준편차 3과 분산 9는 같은 의미이기 때문입니다.
평균 10, 표준편차 3인 정규 분포를 아래 링크를 사용하여 그려보았습니다.
https://onlinestatbook.com/2/calculators/normal_dist.html
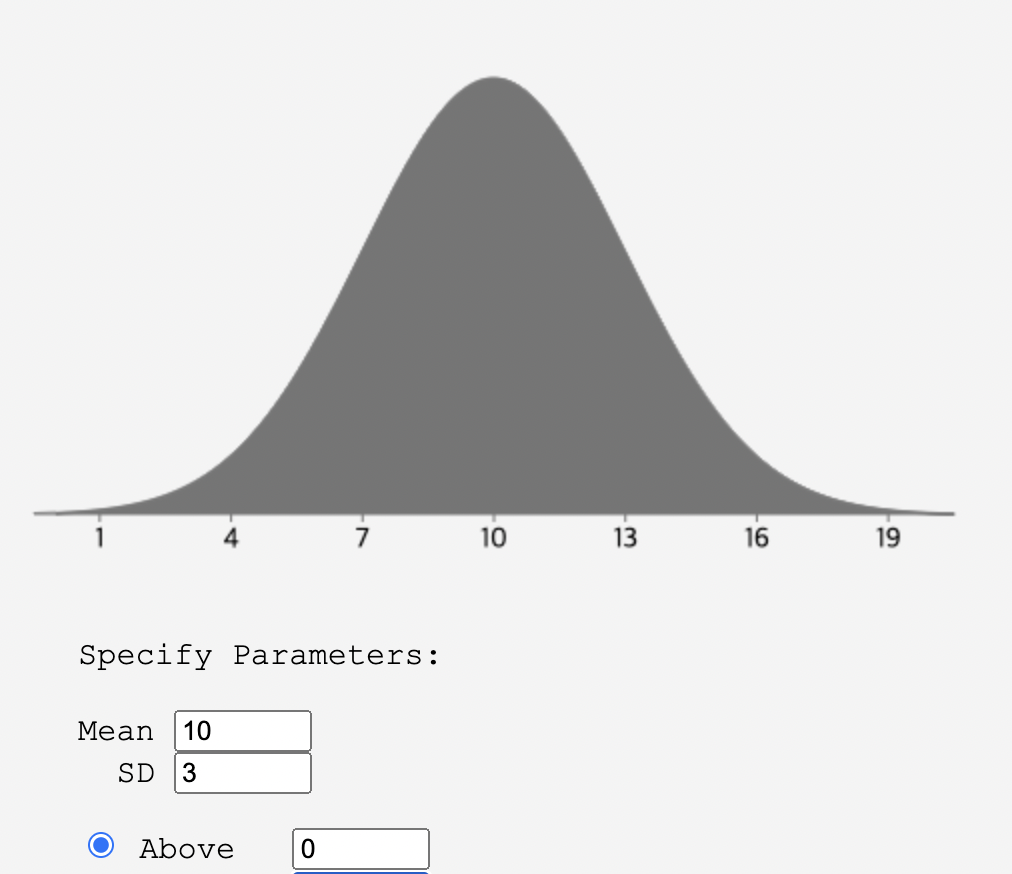
평균과 표준편차는 정규 분포의 형태를 결정하는 두 가지 파라미터입니다.
평균은 정규분포의 중심 위치를 결정하며 표준편차는 정규분포를 그리는 곡선의 너비를 결정합니다. 정규 분포를 구성하는 원소의 개수가 많아질 수록 정규분포의 높이가 높아집니다. 이 부분은 다음 포스트를 통해 확인했습니다.
Matplotlib로 정규 분포 그려보기
https://webnautes.tistory.com/1917
아래 그림처럼 표본의 약 68% 원소가 그래프 중앙에 있는 x좌표가 0인 평균에서 양쪽으로 표준편차를 더하고 뺀 범위(μ ± σ)에 존재하며(어두운 파란색 부분) 표본의 약 95% 원소는 평균에서 양쪽으로 표준편차 2배를 더하고 뺀 범위(μ ± 2σ)에 존재합니다. (중간 파란색과 어두운 파란색 부분) 표본의 대부분의 원소는(99.7%) 평균에서 양쪽으로 표준편차 3배를 더하고 뺀 범위(μ ± 3σ)에 존재합니다.( 밝은 파란색, 중간 파란색, 어두운 파란색 부분)
표본의 원소들을 표준화(standardization) 해야, 아래 그림의 어느 부분에 속하는지 알 수 있습니다.
표준화는 표본의 평균(μ)과 표준편차(σ)를 구한 후, 다음 식에 의해서 구할 수 있습니다.


분산과 표준편차 구하는 예제
개의 키를 측정한 결과가 다음과 같습니다. (개의 어깨까지의 높이를 측정합니다.)
600mm, 470mm, 170mm, 430mm, 300mm
우선 평균을 구합니다.

평균 394와 개들의 키 사이의 차이를 구합니다.
600 - 394 = 206
470 - 394 = 76
170 - 394 = -224
430 - 394 = 36
300 - 394 = -94
분산을 구하기 위해 앞에서 구한 차이를 제곱하여 모두 더한 후, 전체 개수로 나누어 평균을 구합니다.
밀리미터의 제곱을 단위로 사용하기 때문에 개의 키에 비해 값이 너무 높아 개의 키와 비교하는 데 사용할 수 없습니다.

표준 편차는 분산의 제곱근입니다.
개의 키에서 사용한 밀리미터 단위와 비슷하기 때문에 개의 키를 비교하는데 사용할 수 있습니다.

비교해보면 평균 394에서 표준편차 범위 내에 (위로 147, 아래로 147 범위내에) 3마리 개가 포함된 것을 아래 그림에서 볼 수 있습니다.
첫번째 개는 키가 큰 편이고, 세번째 개는 키가 작은 편이라는 것을 알 수 있습니다.

정규 분포에서 평균 ± 1 표준 편차는 전체의 68%라는 점을 상기하면 개의 키 측정값의 약 68%가 이 범위내에 존재한다고 예상할 수 있습니다.

앞에서 본것 처럼 관찰하는 것이 개 5마리의 키라면 상관없지만 더 많은 개가 존재하는데(모집단이라고 합니다.) 그중 5마리만 뽑아서 한다면 계산식이 바뀌어야 합니다.
N 개의 원소가 존재한다고 할 때 모집단에 대한 분산을 계산한다면 N으로 나눕니다.
하지만 모집단에서 뽑은 표본에 대한 분산을 계산한다면 N-1로 나누어야 합니다.
평균과 표준편차를 구하는 방법은 동일합니다.
예를 들어 모집단에서 5마리를 뽑은 표본에 대해 분산을 구할 때에는 5 대신 4로 나눕니다. 평균을 구할때는 모집단에서 한 것과 동일하게 전체 원소 개수인 5로 나눕니다. 표준편차도 모집단에서 한것과 동일한 방식으로 계산합니다.
평균

분산

표준편차

제곱을 하는 이유
평균으로부터의 차이를 모두 더하게 되면 아래의 경우처럼 합이 0이 되는 경우가 있습니다.


절대값을 취하게 되면 계산 결과가 0이 되지 않기 때문에 이 문제가 해결되는 것처럼 보입니다.


하지만 아래 경우처럼 평균과의 차이가 앞의 경우보다 더 큰 값이 포함되어 있는데도( 더 퍼져있다고도 합니다.) 계산결과 앞과 동일한 값을 가질 수 있습니다.


평균과의 차이 값을 각각 제곱하여 더해주어 계산 후, 제곱근을 취하여 표준편차를 구하면 앞에서 본 두가지에 대한 계산 결과에 차이가 생깁니다.




표준 편차는 원소들과 평균의 차이가 많이날 수록 더 커집니다. 첫번째 보다 두번째 경우가 더 퍼져있기 때문에 계산결과 더 높은 값을 가집니다.
참고
https://www.mathsisfun.com/data/standard-deviation.html
'Deep Learning & Machine Learning > 딥러닝&머신러닝 개념' 카테고리의 다른 글
| 기대값이란 (0) | 2023.11.05 |
|---|---|
| 신경망(neural networks)에서 편향(bais)의 역할 (0) | 2023.10.28 |
| 정규화(Normalization), 표준화(standardization), 이상치(outlier) 제거 (0) | 2023.10.23 |
| XGBoost 개념 정리 (0) | 2023.10.18 |
| 난수 생성에서 시드(seed) 사용하는 이유 (0) | 2023.10.12 |




