

아래 링크들을 참고하여 랜덤 포레스트에 대해 간단히 정리했습니다.
https://www.section.io/engineering-education/introduction-to-random-forest-in-machine-learning/
https://wooono.tistory.com/104
2022. 10. 13 최초작성
랜덤 포레스트(random forest)
랜덤 포레스트는 회귀(regression) 및 분류(classification) 문제를 해결하는 데 사용할 수 있는 머신 러닝(machine learning) 기법입니다. 여러 개의 의사 결정 트리(decision trees)로 구성되는데 각각의 의사 결정 트리는 출력 결과를 내놓습니다. 최종 결과를 얻기 위해 앙상블 기법중 하나인 배깅(bagging)을 사용합니다.
배깅 방식은 여러 개의 모델이 독립적입니다. 여러 개의 모델을 만들지만 이 과정에서 각각의 모델들은 서로의 영향을 받지 않습니다. 여러 개의 모델을 만들기 위해 각 모델별로 임의의 데이터 세트를 생성하는데 이 때 복원 추출(하나를 뽑을때마다 뽑은걸 다시 넣어서 다음번 뽑을때 다시 후보가 될 수 있게함)을 사용하여 무작위로 N개를 선택하여 데이터 세트를 생성합니다.
랜덤 포레스트를 사용해서 풀고자하는 문제가 분류인 경우에는 다수의 결과를 따라 최종 결정이되고 회귀인 경우에는 의사 결정 트리의 결과들을 평균내어서 최종 결정을 정합니다.
의사 결정 트리
특정 기준(질문)에 따라 데이터를 분리하는 모델을 의사 결정 트리라고 합니다.
의사결정 트리는 의사결정 노드(decision nodes), 리프 노드(leaf nodes), 루트 노드(root node)로 구성됩니다. 의사 결정 노드와 루트 노드에는 특정 기준(질문)이 주어지며 리프 노드에는 최종 출력이 주어집니다.
특정 기준(질문)이 의사 결정 트리의 노드마다 주어지며 특정 기준(질문)을 만족하는지 여부에 따라 노드에서 데이터가 둘로 분리되어 자식 노드로 데이터가 전달됩니다. 자식 노드에서 특정 기준(질문)에 따라 데이터가 다시 분리됩니다. 이런 데이터 분리 과정은 리프 노드에 도달할 때까지 계속됩니다. 리프 노드에서는 데이터가 더 이상 분리되지 않습니다.

예를 들어 의사 결정 트리의 동작 원리를 살펴보겠습니다.

데이터 세트는 2개의 1과 5개의 0으로 구성되어 있다고 가정합니다. 숫자에는 특징으로 색깔과 밑줄 여부가 주어집니다. 이 특징들을 사용하여 데이터 세트를 여러 개의 클래스로 분리하려고 합니다.

데이터 세트를 구성하는 숫자들의 색깔을 살펴보면 0의 경우 하나를 제외하고 모두 파란색이므로 분할하기에 좋은 특징으로 보입니다. 따라서 루트 노드에 주어질 질문으로 “빨간색 입니까?" 라는 질문을 사용할 수 있습니다.
루트 노드에서 이 질문을 기준으로 데이터가 둘로 분리됩니다. 기준을 충족하는 데이터는 Yes가 되어 왼쪽 자식노드로 이동하고 그렇지 않은 데이터는 No가 되어 오른쪽 자식 노드로 이동합니다.
오른쪽 자식 노드로 이동한 데이터는 모두 0이고 밑줄도 없으므로 주어진 특징으로 데이터를 더 이상 분리할 수 없습니다. 따라서 이 노드는 리프 노드가 됩니다. 왼쪽 자식 노드로 이동한 데이터는 색깔은 빨간색으로 동일하지만 밑줄이 있는 숫자와 없는 숫자가 뒤섞여 있기 때문에 데이터를 더 분리할 수 있습니다.

이제 왼쪽 자식 노드의 특징으로 "밑줄이 있습니까?"라고 물을 수 있습니다.
이 노드를 기준으로 데이터가 둘로 분리됩니다. 밑줄이 그어진 두 개의 1은 Yes가 되어 왼쪽 자식 노드로 이동하고 밑줄이 없는 0은 No가 되어 오른쪽 자식 노드로 이동합니다. 이제 모든 자식 노드는 데이터를 더 이상 분리할 수 없으므로 둘 다 리프 노드입니다. 데이터의 모든 분리가 끝났습니다.

이처럼 의사 결정 트리의 기본 아이디어는 최종적으로 리프 노드에 여러가지 특징을 갖는 데이터가 섞여있지 않도록 하는 것입니다.

불순도 (Impurity)
의사 결정 트리에서 노드를 기준으로 데이터를 분리하는 기준을 선택하기 위해서는 불순도(impurity)라는 개념을 사용합니다. 노드에 있는 데이터가 얼마나 섞여 있는지를 뜻합니다. 다양한 특징을 갖는 데이터가 섞여 있을수록 불순도가 높아집니다.
노드에 데이터 분리 기준을 설정할 때 현재 노드의 불순도보다 자식 노드의 불순도가 낮아지도록 해야 합니다. 현재 노드의 불순도와 자식 노드의 불순도 차이를 정보 획득(Information Gain)이라고 합니다. 예를 들어 불순도가 1.0인 상태에서 0.7인 상태로 바뀌었다면 정보 획득은 0.3입니다.
불순도를 수치로 나타내는 함수에는 지니(Gini)와 엔트로피(Entropy)가 있습니다.

의사 결정 트리 구성 단계
- 현재 노드에 주어진 특징에 대한 불순도를 계산합니다.
- 특징에 따라 데이터를 둘로 분리한 후, 자식 노드의 불순도를 계산합니다.
- 특징에 따라 데이터를 둘로 분리하기 전 후의 불순도를 대한 정보 획득을 계산한 후 정보 획득이 최대가 되는 특징을 사용하여 데이터를 분리합니다. 데이터 분리 전후의 불순도의 차이가 큰 특징을 사용하는 것입니다.
- 모든 리프 노드의 불순도가 0이 될 때까지 1, 2,3을 반복 수행합니다.
살펴본 과정에 대한 예시를 아래 블로그 글에서 잘 설명하고 있으니 확인해보세요.
https://wooono.tistory.com/104
의사 결정 트리와 랜덤 포레스트의 차이
훈련 데이터가 원하는 의도대로 분리되도록 하는 역할을 하는 특정 기준(질문) 또는 정답을 노드에 배치하는 작업을 의사 결정 트리에서는 사람이 하지만 랜덤 포레스트에서는 무작위로 수행됩니다.
랜덤 포레스트 예시
풀고자 하는 문제가 분류인 경우 의사 결정 트리는 대다수의 의사 결정 나무가 선택한 출력으로 결정되며 풀고자 하는 문제가 회귀인 경우에는 모든 의사 결정 나무의 평균으로 출력이 결정됩니다.
고객이 휴대전화를 구매할지 여부를 예측한다고 가정해 보겠습니다.
의사 결정 트리의 루트 노드와 의사 결정 노드는 휴대전화의 특징이 됩니다. 리프 노드는 구매 여부를 의미하는 최종 출력을 나타냅니다. 선택을 결정하는 주요 특징에는 가격( Price of the phone), 메모리(RAM), 내부 저장소(Internal storage)가 있습니다.
의사 결정 트리는 다음과 같습니다.
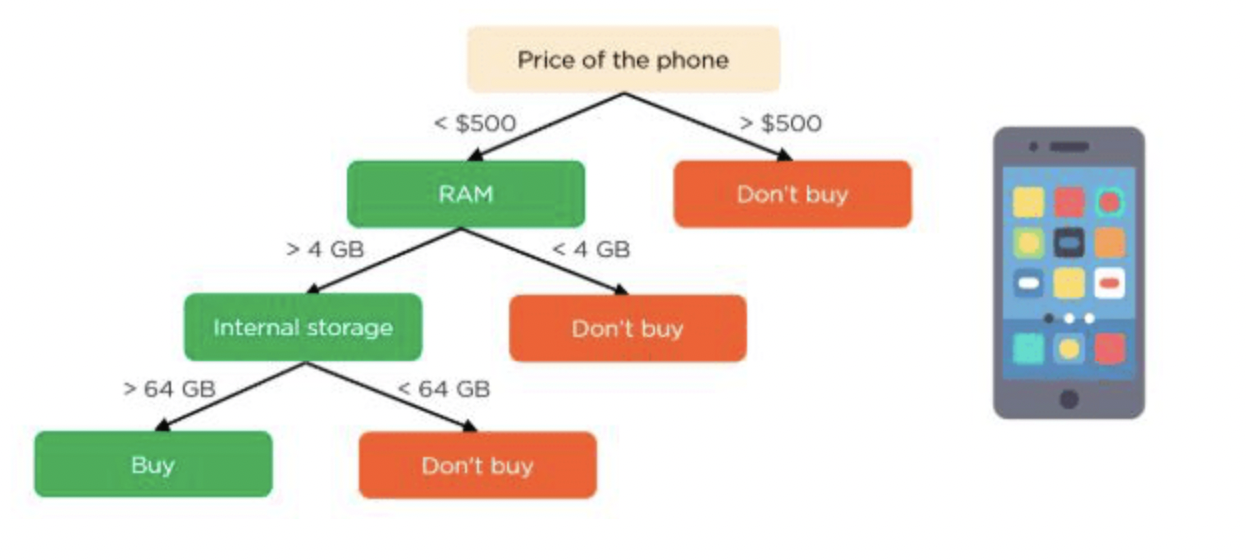
랜덤 포레스트를 구성하는 의사 결정 트리가 4개라고 가정을 해보면 위와 같은 트리가 4개 존재하는 것입니다.
랜덤 포레스트에 포함되어 있는 각각의 의사 결정 트리는 주어진 4가지 특징을 무작위로 선택하여 노드를 분할합니다. 최종 예측은 4개의 트리의 결과를 기반으로 선택됩니다.
분류 문제이므로 다수의 의사 결정 트리에서 선택한 결과가 최종 선택이 됩니다. 3개의 의사 결정 트리가 구매를 예측하고 1개의 의사 결정 트리가 구매하지 않을 것으로 예측했다면 최종 예측은 구매가 됩니다.
랜덤 포레스트 사용을 피해야 하는 경우
- 랜덤 포레스트를 회귀에 사용할 경우 외삽(Extrapolation)에는 사용하지 않는 것이 좋습니다. 예를 들어 외삽은 올 여름 8월에 태풍이 왔으니 내년 여름 8월에도 태풍이 올거라고 예측하는 것입니다.
- 랜덤 포레스트는 데이터가 매우 희소할 때 좋은 결과를 보여주지 못합니다.
'Deep Learning & Machine Learning > 강좌&예제 코드' 카테고리의 다른 글
| 상관 계수(Correlation coefficient) 개념 (0) | 2023.10.23 |
|---|---|
| 정규 분포와 연속 확률 분포 개념 (0) | 2023.10.23 |
| 미분으로 곡선의 노이즈 양 측정하는 파이썬 예제코드 (0) | 2023.10.18 |
| 데이터셋을 일정비율로 분리하는 : train_test_split 예제 (0) | 2023.10.17 |
| Keras 모델( .h5)을 onnx로 변환 및 OpenCV DNN에서 사용하기 (0) | 2023.10.10 |





