표준정규분포 표준화 (standardization)
상관 계수(Correlation coefficient) 중 하나인 피어슨 상관 계수(Pearson Correlation Coefficient)의 개념에 대해 정리했습니다.
2022. 5. 23 최초작성
상관 계수
상관 계수는 두 변수 간의 연관성 강도를 측정합니다. 본 글에서는 상관 계수 중 하나인 피어슨 상관 계수에 대해 알아봅니다. 피어슨 상관 계수는 두 변수 간의 선형 연관 강도를 측정합니다.
피어슨 상관 계수
피어슨 상관 계수는 두 변수 간의 선형 연관 강도를 측정합니다.
- 상관 계수의 범위는 항상 -1과 1 사이입니다.
- 계수의 부호는 관계의 방향을 알려줍니다. 양수 값은 두 변수가 같은 방향으로 함께 변경됨을 의미하고 음수 값은 두 변수가 반대 방향으로 변경됨을 의미합니다.
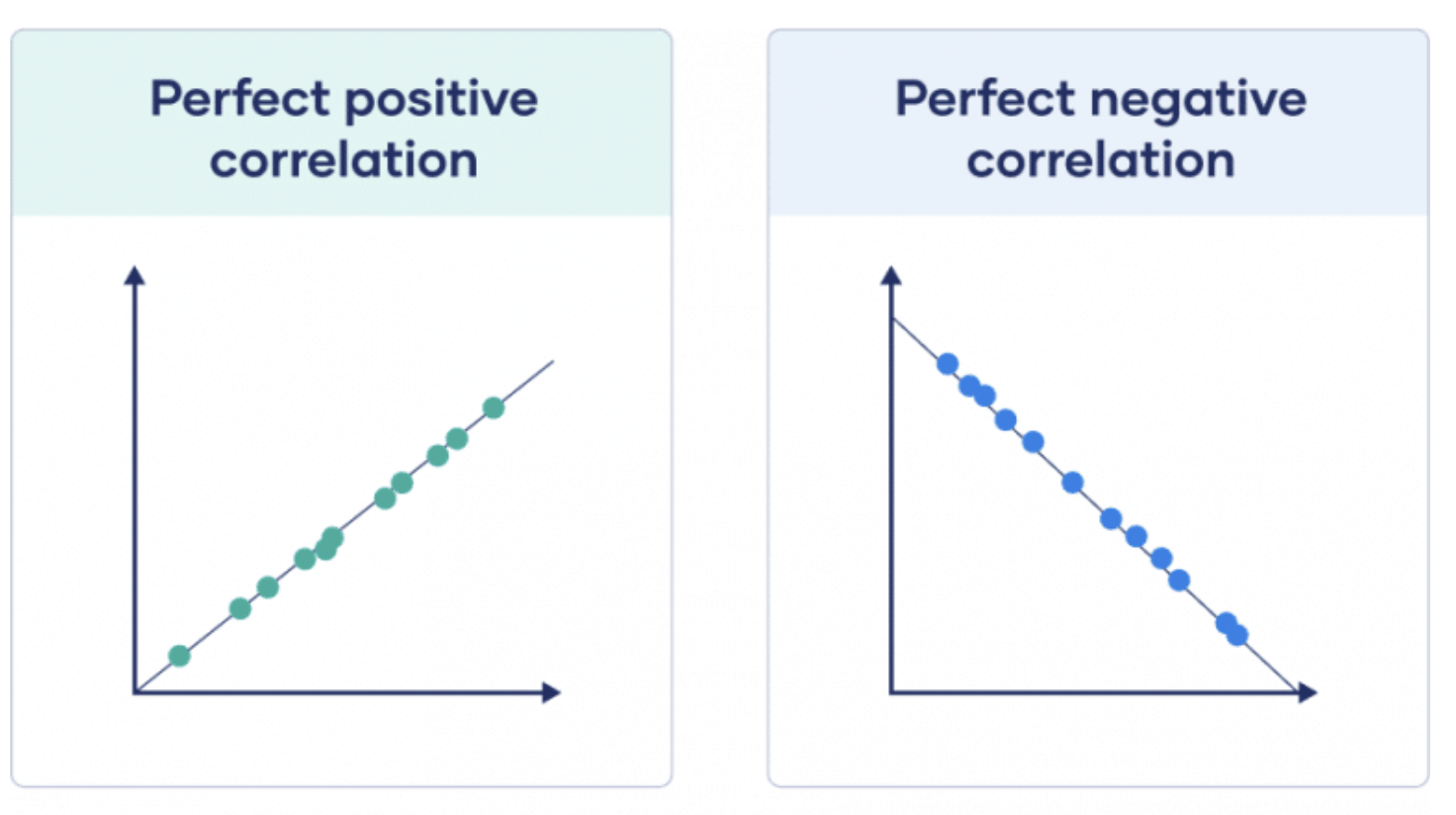
- 양의 상관관계는 한 변수가 커지면 다른 변수도 커지고, 한 변수가 작아지면 다른 변수도 작아지는 경향이 있음을 의미합니다. 양의 상관관계의 최대값은 1입니다.(perfect positive correlation)
- 음의 상관관계는 한 변수가 커지면 다른 변수는 작아지는 경향이 있음을 의미합니다. 음의 상관관계의 최소값은 -1입니다. (perfect negative correlation)
- 상관 관계값이 0이면(zero correlation) 두 변수사이에 관계가 없다는 의미입니다. 한 변수가 변경되어도 다른 변수에 영향을 주지 않습니다.
- 상관계수 값의 절대값은 상관 관계의 크기를 의미합니다. 절대값이 클수록 상관 관계가 더 강해집니다.
- 가장 강한 선형 관계는 -1 또는 1의 상관 계수로 표시됩니다.
- 가장 약한 선형 관계는 0에 가까운 상관 계수로 표시됩니다.

피어슨 상관 계수는 선형 관계만 측정하기 때문에 상관 관계가 0이라고 해서 두 변수 간의 관계가 0인 것은 아닙니다.
두 변수가 제로 선형 관계(zero linear relationship)이고 동시에 곡선 관계(curvilinear relationship)가 강할 수 있습니다.
곡선 관계는 두 변수 간의 관계 유형으로, 예를 들어 U자형 곡선의 경우 하나의 변수가 증가하면 다른 유형의 곡선 관계는 특정 지점까지 감소한 다음 두 변수가 함께 증가하는 것입니다. 예를 들어 직원의 유쾌함과 고객 만족도가 있습니다. 서비스 직원이 쾌활할수록 고객 만족도는 높지만 특정 지점까지만 서비스 직원이 너무 쾌활하면 고객의 만족 수준이 떨어질 수 있습니다.
상관 계수는 기술 통계이며 모집단에 대해 추론하지 않고 샘플 데이터를 요약합니다.
상관 계수는 두 변수 간의 관계를 요약할 때 이변량 통계이고, 두 개 이상의 변수가 있을 때 다변수 통계입니다.
상관 계수가 표본 데이터를 기반으로 하는 경우 결과를 모집단에 일반화하려면 추론 통계가 필요합니다. F 검정(F test) 또는 t 검정(t test)을 사용하여 결과의 통계적 유의성을 알려주는 검정 통계량을 계산할 수 있습니다.
피어슨 상관 계수는 두 변수의 공분산(covariance) 을 각각의 표준 편차의 곱으로 나눈 값입니다. 즉 두 변수의 공분산과 표준 편차의 곱 사이의 비율입니다. 따라서 본질적으로 공분산의 정규화된 값을 계산합니다. 항상 -1과 1 사이의 값을 갖습니다. 공분산 자체와 마찬가지로 피어슨 상관 계수는 두 변수의 선형 상관만 측정됩니다.

피어슨 상관계수를 사용하려면 데이터가 충족해야 하는 가정입니다.
- 두 변수가 같은 측정의 구간 또는 비율 수준에 있습니다.
- 두 변수의 데이터는 정규 분포를 따릅니다.
- 데이터에 이상값(outlier)이 없습니다.
- 데이터는 무작위 또는 대표 샘플(representative sample)에서 가져온 것입니다. 대표 샘플은 모집단의 속성을 가진 샘플을 의미합니다.
- 두 변수가 선형 관계를 가져야 합니다.
상관 계수를 사용한 연구 비교
상관 계수는 결과의 실질적인 의미를 알려주는 효과의 크기를 측정할 수 있습니다. 왜냐하면 상관 계수는 단위가 없으므로 연구 간의 계수를 직접 비교할 수 있습니다.
상관 계수 사용
상관 관계 연구에서는 한 변수의 변경 사항이 다른 변수의 변경 사항과 관련되어 있는지 여부를 조사합니다.
예를 들어 고등학교 SAT 점수와 대학의 학업 성적 GPA 사이에 관련이 있는지 조사합니다. 양의 상관 관계가 있다고 예측합니다. SAT 점수가 높을수록 대학 GPA가 높고 SAT 점수가 낮을수록 대학 GPA가 낮습니다.
데이터 수집 후 x축에 하나의 변수를 표시하고 y축에 다른 변수를 표시하여 산점도로 데이터를 시각화할 수 있습니다. 어느 축에 어떤 변수를 배치하든 상관 없습니다.
그래프에 패턴을 시각적으로 그려 확인하고 변수 사이에 선형 또는 비선형 패턴이 있는지 여부를 결정합니다. 선형 패턴은 데이터 포인트 사이에 가장 잘 맞는 직선을 맞출 수 있음을 의미하는 반면, 비선형 또는 곡선 패턴은 U자형 또는 곡선과 같은 모든 종류의 다양한 모양을 취할 수 있습니다.
5,000명의 대졸자 표본을 수집하여 고등학교 SAT 점수와 대학 GPA에 대해 조사합니다. 선형 패턴을 확인하기 위해 산점도의 데이터를 시각화합니다.

피어슨 상관 계수 시각화
두 변수 사이에 선형 관계가 있는 경우 산점도에서 모든 샘플을 고려하는 최적의 직선을 그릴 수 있습니다. 샘플에 대해 선형 회귀를 수행하면 구할 수 있는 직선입니다.
상관 계수는 데이터가 직선에 얼마나 가깝게 위치하고 있는지 알려줍니다.
샘플들이 직선에 가까이 있을 수록 상관 계수의 절대값이 더 높아지고 선형 상관 관계가 더 강해집니다.
모든 샘플들이 직선에 위에 있다면 완벽한 상관 관계가 있습니다.
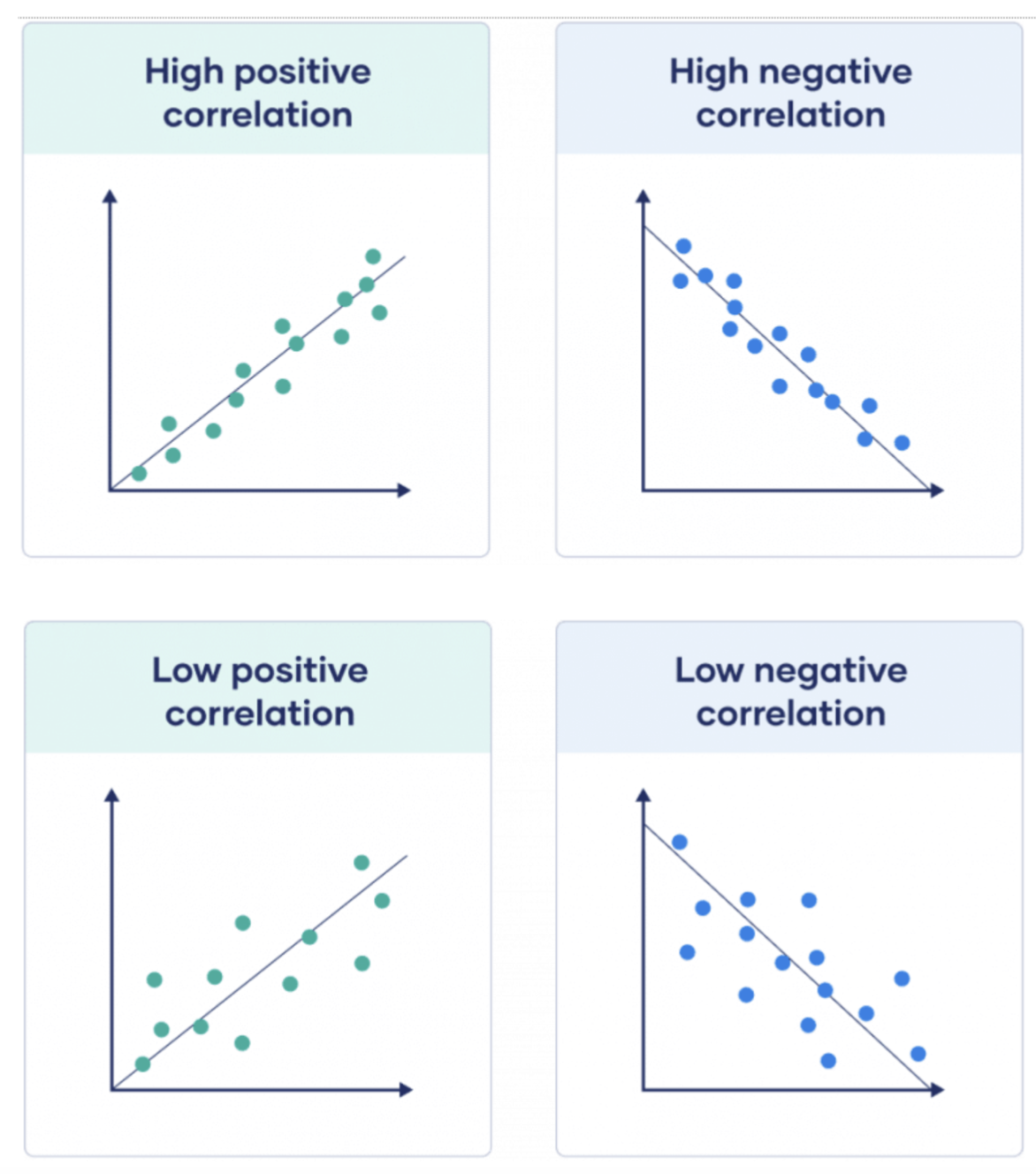
모든 샘플들이 직선에 가까울 수록 상관 계수의 절대값이 높습니다. 아래 첫번째 줄 그림이 두번째 줄 그림보다 상관계수의 절대값이 높습니다.
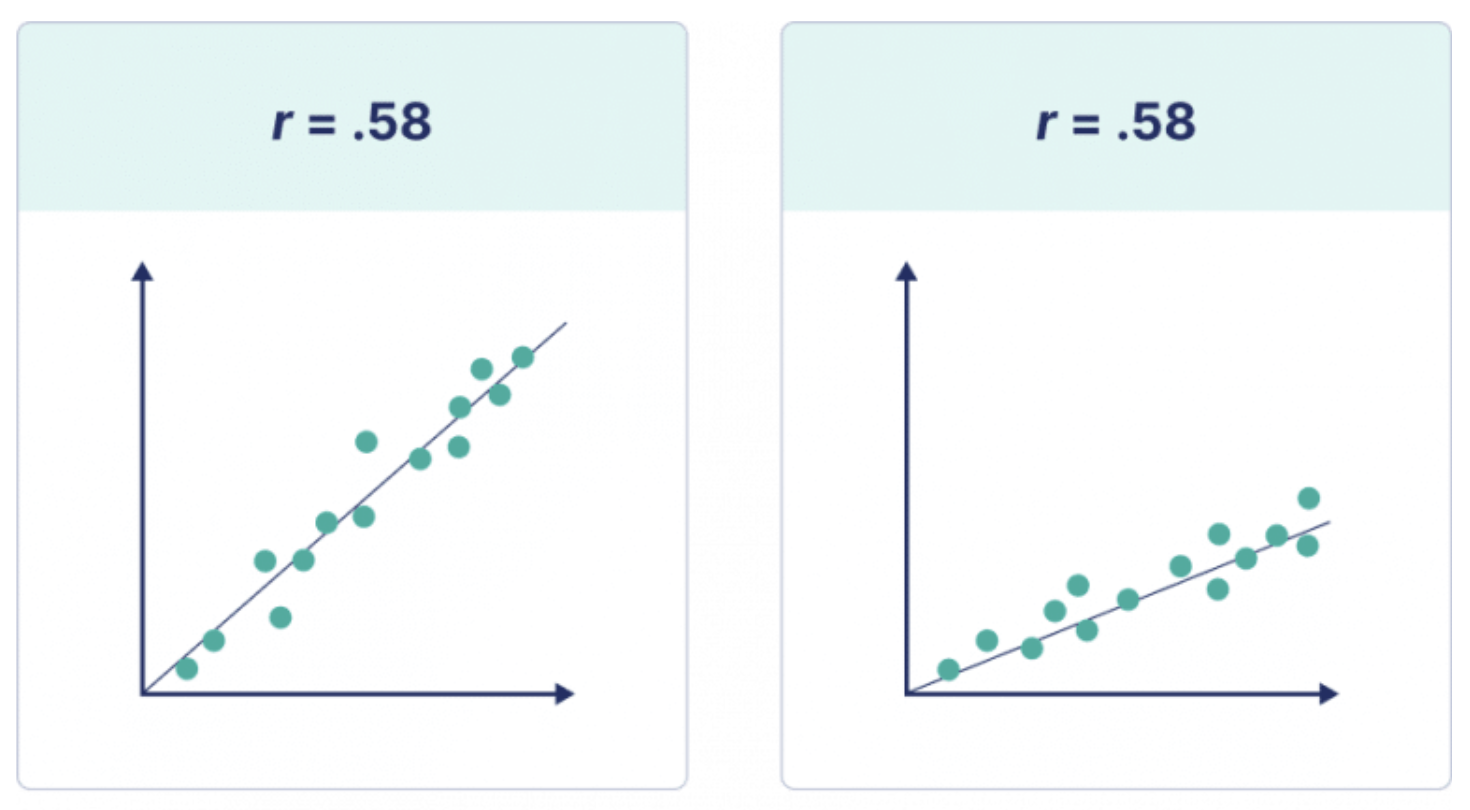
직선의 기울기는 상관 계수 값과 관련이 없습니다. 상관 계수는 데이터가 직선에 얼마나 가깝게 분포하는지 알려줄 뿐이므로 상관 계수가 동일한 두 데이터 세트에 해당되는 직선의 기울기가 다를 수 있습니다.
직선의 기울기를 찾으려면 회귀 분석을 수행해야 합니다.
아래 그림에서 상관 계수 r 이 동일하지만 두 직선의 기울기가 다른 것을 볼 수 있습니다.
참고
https://www.scribbr.com/statistics/correlation-coefficient/
https://alleydog.com/glossary/definition.php?term=Curvilinear+Relationship
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
https://ko.wikipedia.org/wiki/피어슨_상관_계수