AUC - ROC Curve 이해하기
AUC - ROC Curve에 대해 다루고 있습니다.
2022. 4. 26 최초작성
2024. 4. 1
아래 링크의 원문을 바탕으로 이해한 내용을 추가하여 작성되었습니다.
https://towardsdatascience.com/understanding-auc-roc-curve-68b2303cc9c5
추가로 참고한 사이트입니다.
https://bioinformaticsandme.tistory.com/148
머신 러닝의 분류 문제에서 성능을 확인하거나 시각화가 필요할 때 AUC(Area Under Curve) - ROC(Receiver Operating Characteristics) Curve를 사용합니다.
혼동행렬(Confusion Matrix)
TP, FP, TN, FN - 4가지 경우는 다음 두가지를 기준으로 합니다.
- Positive는 양성으로 판정을 의미, Negative는 음성으로 판정을 의미.
- True는 판정이 옳았음을 의미, False는 판정이 틀렸음을 의미.

AUC - ROC Curve
AUC - ROC Curve는 임계값(threshold)를 변화시키면서 분류 문제에 대한 성능을 측정합니다.
ROC는 확률 곡선(probability curve)이고 AUC는 분리의 정도를 나타냅니다.
ROC 곡선 아래에 있는 면적이 AUC입니다.
AUC - ROC Curve는 모델이 클래스를 얼마나 잘 분류할 수 있는지 알려줍니다.
AUC가 높을수록 모델이 0 클래스를 0으로, 1 클래스를 1로 예측을 잘한다는 것을 의미합니다.
또는 AUC가 높을수록 모델이 질병이 있는 환자와 질병이 없는 환자를 더 잘 구별할 수 있습니다.
ROC 곡선은 TPR(True Positive Rate)이 y축에 있고 FPR(False Poritive Rate)이 x축에 있는 좌표평면에 그려집니다. FPR의 변화에 따른 TPR의 변화를 보여줍니다.

AUC - ROC Curve에서 사용되는 용어 정의
TPR (True Positive Rate) / Recall /Sensitivity

Specificity

FPR(False Positive Rate)

모델의 성능을 추측하는 방법
성능 좋은 모델은 AUC가 1에 가까우며 클래스 분류를 잘합니다.
성능 안좋은 모델은 AUC가 0에 가까우면 클래스 분류를 최악으로 잘못합니다.
즉 0을 1로 1을 0으로 예측하는 모델입니다.
AUC가 0.5이면 모델에 클래스 분류 능력이 전혀 없다는 것을 의미합니다.
ROC는 확률 곡선입니다. 이러한 확률의 분포를 그래프화하여 살펴 보겠습니다.
아래 그림에서 빨간색 분포 곡선은 양성 클래스(True Positive, positive class, 병에 걸린 사람)이고 녹색 분포 곡선은 음성 클래스(True Negative, negative class, 병에 안걸린 사람)입니다.
아래 경우는 이상적인 상황입니다. 두 곡선이 전혀 겹치지 않기 때문에 모델이 양성 클래스와 음성 클래스를 완벽하게 구분할 수 있습니다.
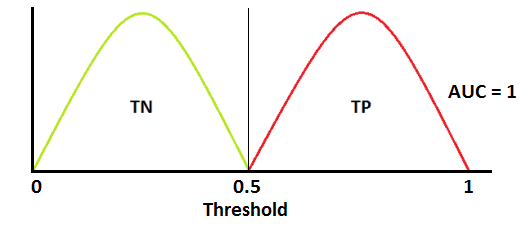
이 경우 ROC Curve는 왼쪽 상단에 있는 (0,1)을 지나갑니다.
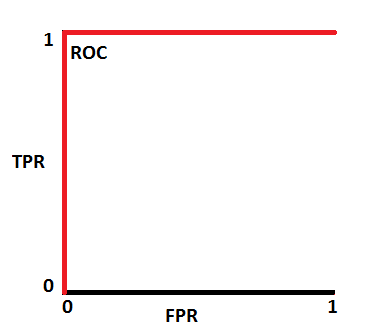
두 분포가 겹치면 1종 오류(type 1 error)와 2종 오류(type 2 error)가 발생합니다.
임계값(threshold)에 따라 1종 오류와 2종 오류를 최소화하거나 최대화할 수 있습니다. 아래 그래프처럼 AUC가 0.7이면 모델이 양성 클래스와 음성 클래스를 구별할 수 있는 확률이 70%임을 의미합니다.
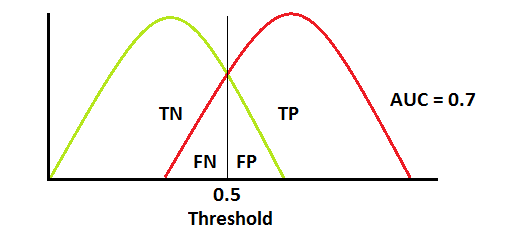
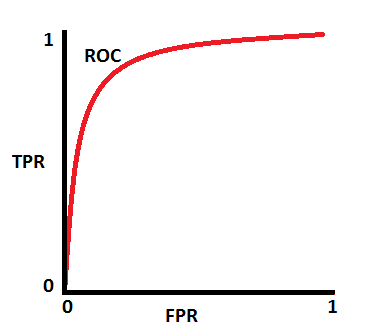
혼동행렬에서 False Positive가 1종 오류, False Negative가 2종 오류 입니다. 1종 오류(False Positive, α error) - 실제 음성인 것을 양성으로 판정 2종 오류(False Negative, β error) - 실제 양성인 것을 음성으로 판정 1 종 오류(α error)와 2종 오류(β error) 확률은 트레이드 오프라서 하나가 커지면, 나머지가 작아집니다. 일반적으로 α error에 기준을 두고 원하는 성능을 얻을 수 있도록 조정합니다. |
AUC가 약 0.5일 때 모델은 양성 클래스와 음성 클래스를 구별하는 판별 능력이 없습니다.
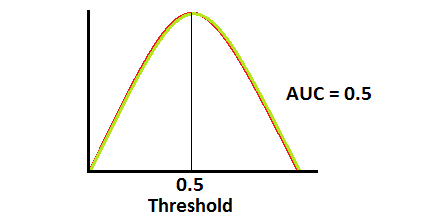
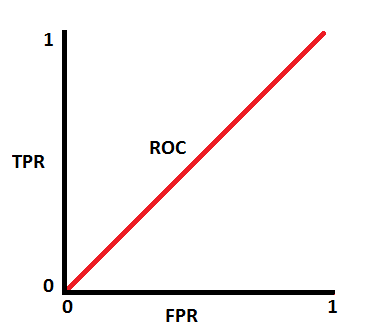
AUC가 0에 가까우면 모델은 클래스를 반대로 예측합니다. 이는 모델이 음성 클래스를 양성 클래스로 예측하고 그 반대의 경우도 마찬가지임을 의미합니다.


Sensitivity와 Specificity, FPR와 Threshold 사이의 관계
민감도(Sensitivity)와 특이도(Specificity)는 서로 반비례합니다.
따라서 Sensitivity를 높이면 Specificity는 감소하고 그 반대의 경우도 마찬가지입니다.
Sensitivity 올리면 Specificity 떨어짐
Sensitivity 내리면 Specificity 올라감
임계값을 낮추면 더 많은 양성 값을 얻게 되므로 민감도는 증가하고 특이도는 감소합니다.
임계값을 높이면 더 많은 음성 값을 얻게 되므로 특이도는 높아지고 민감도는 낮아집니다.
FPR은 1 - 특이성이기 때문에 TPR을 높이면 FPR도 증가하고 그 반대의 경우도 마찬가지입니다.
TPR 올리면 FPR 올라감
TPR 떨어지면 FPR 떨어짐
ROC 곡선 그려보기
가상의 실제 레이블과 예측 확률을 사용하여 ROC 곡선을 그려주는 예제 코드입니다.
| import numpy as np from sklearn.metrics import roc_curve, auc import matplotlib.pyplot as plt y_true = np.array([0, 0, 1, 1]) # 실제 레이블 y_scores = np.array([0.1, 0.4, 0.35, 0.8]) # 예측 확률 # ROC 곡선 계산 fpr, tpr, thresholds = roc_curve(y_true, y_scores) # fpr과 tpr 값을 출력합니다. for i, (fpr_i, tpr_i) in enumerate(zip(fpr, tpr)): print(f'[{i}] fpr_{i}={fpr_i}, tpr_{i}={tpr_i}') # AUC 계산 roc_auc = auc(fpr, tpr) # ROC 곡선 그리기 plt.figure() plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc) plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--') plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('Receiver Operating Characteristic Example') plt.legend(loc="lower right") plt.show() |
실행하면 다음처럼 fpr과 tpr이 출력됩니다.
[0] fpr_0=0.0, tpr_0=0.0
[1] fpr_1=0.0, tpr_1=0.5
[2] fpr_2=0.5, tpr_2=0.5
[3] fpr_3=0.5, tpr_3=1.0
[4] fpr_4=1.0, tpr_4=1.0
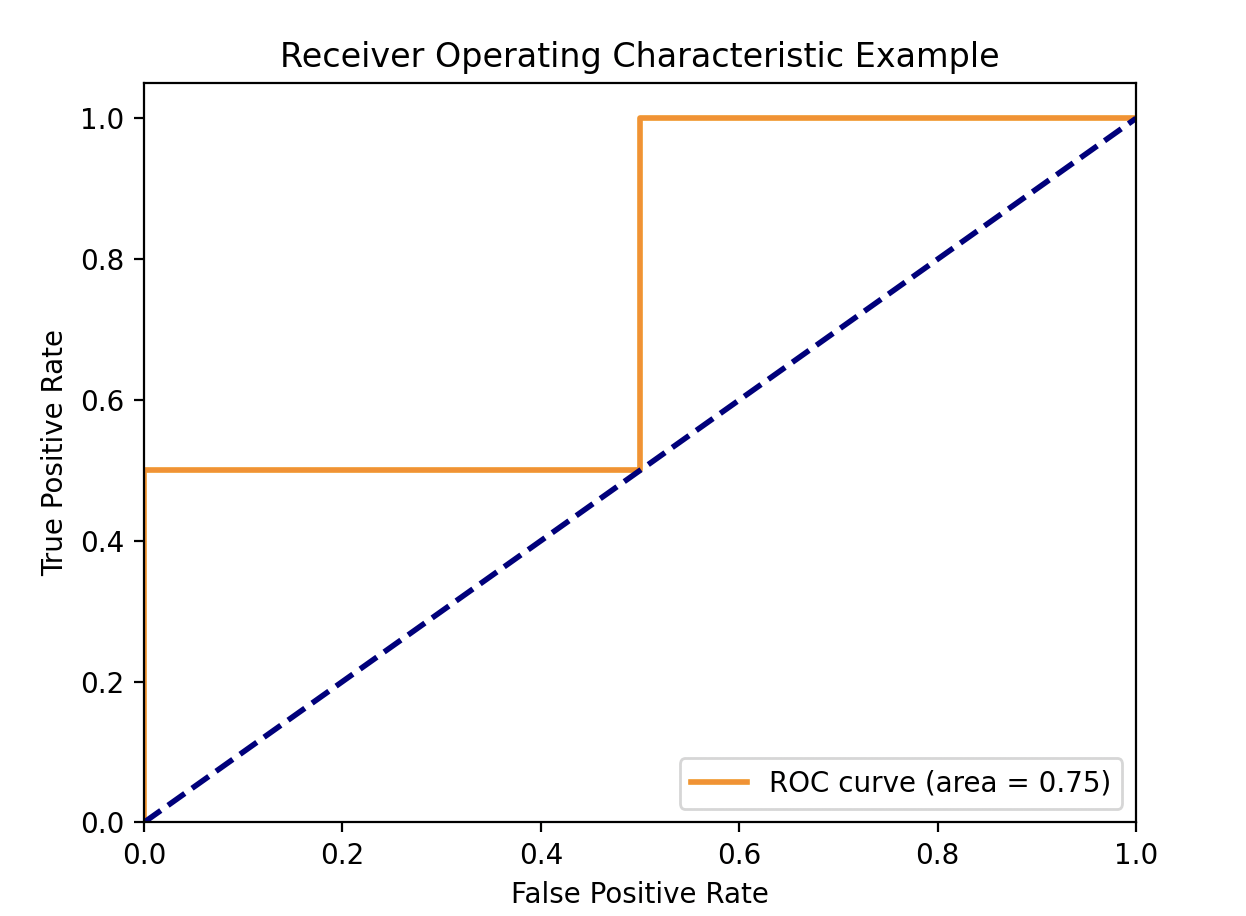
위에 출력된 fpr(False Positive Rate)와 tpr(True Positive Rate) 쌍이 아래에 주황색으로 그려진 ROC 그래프의 좌표와 일치하는 것을 볼 수 있습니다.
다중 클래스 모델에서 AUC - ROC Curve
다중 클래스 모델에서 One vs ALL 방법론을 사용하여 N개의 클래스에 대한 N개의 AUC - ROC Curve을 그릴 수 있습니다.
One vs ALL는 관심있는 클래스와 관심 있는 클래스외에 나머지 모든 클래스를 하나로 묶은 것을 가지고 이진 분류처럼 보는 것입니다.
예를 들어, X, Y, Z라는 세 개의 클래스가 있는 경우 Y와 Z를 하나로 묶고 X와의 ROC, X와 Z를 하나로 묶고 Y와의 ROC, Y와 X를 하나로 묶고 Z와의 ROC를 구합니다.