Matplotlib로 FFT 그려보기

Python/Matplotlib

Matplotlib로 FFT 그려보기

webnautes 2022. 1. 17. 18:06

Matplotlib를 사용하여 FFT를 그려보았습니다.

2021. 12. 18 최초작성

2021. 12. 31 예제 코드 추가

2021. 01. 17 예제 코드 추가

아직 정확히 개념이 잡힌 상태가 아니라서 틀린점이 있을 수 있으니 참고용으로만 사용하세요.

다음 두 개의 sin 그래프를 FFT로 변환하여 그려봅니다.

오른쪽의 진폭이 2배 더 큽니다.

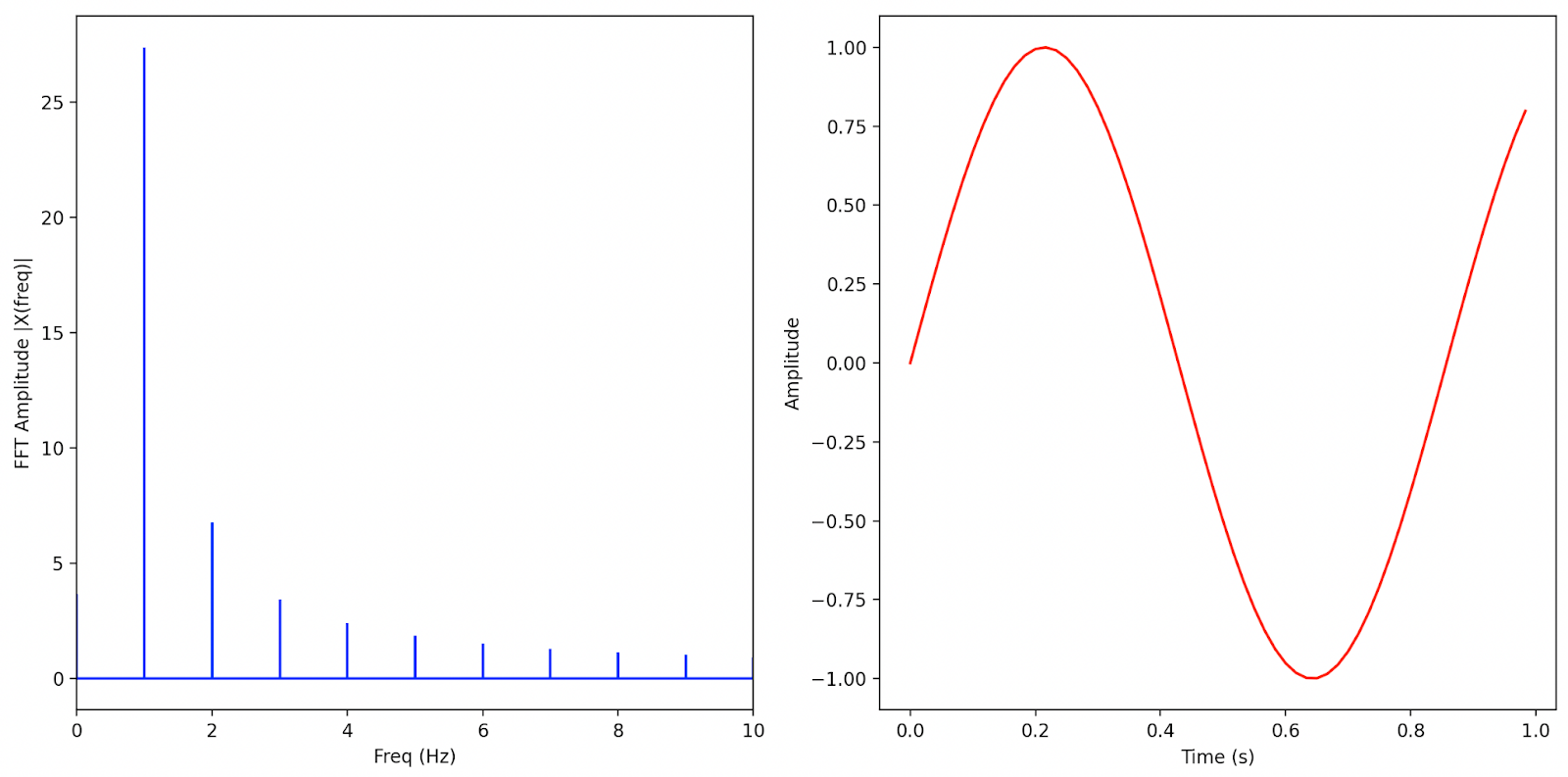
왼쪽은 FFT로 변환한 결과이며 오른쪽은 FFT 결과를 역변환하여 얻은 원래 파형을 그린것입니다.

두 개의 sin 그래프의 FFT 결과에서 다른 점은 1Hz에서의 높이가 원래 파형의 배수만큼 다른 것입니다.

원래 그래프에서 2배 차이가 났었는데 FFT의 1Hz에서의 높이도 2배 차이입니다.

전체 소스코드입니다.

# 참고 : https://pythonnumericalmethods.berkeley.edu/notebooks/chapter24.04-FFT-in-Python.html

import numpy as np
from matplotlib import pyplot as plt
from numpy.fft import fft, ifft

x = np.arange(0, 60)
y1 = np.sin(7*x * np.pi / 180. )
y2 = np.sin(7*x * np.pi / 180. + 3 ) * 2

plt.figure(figsize = (12, 6))

plt.subplot(121)
plt.plot(x, y1, color='r')

plt.subplot(122)
plt.plot(x, y2, color='b')
plt.show()

data = [y1, y2]

for d in data:

    x = d
    sr = 60 # sampling rate
    ts = 1.0/sr # sampling interval
    t = np.arange(0, 1, ts)

    X = fft(x)
    N = len(X)
    n = np.arange(N)
    T = N/sr
    freq = n/T

    plt.figure(figsize = (12, 6))
    plt.subplot(121)

    plt.stem(freq, np.abs(X), 'b', markerfmt=" ", basefmt="-b")
    plt.xlabel('Freq (Hz)')
    plt.ylabel('FFT Amplitude |X(freq)|')
    plt.xlim(0, 10)

    plt.subplot(122)
    plt.plot(t, ifft(X), 'r')
    plt.xlabel('Time (s)')
    plt.ylabel('Amplitude')
    plt.tight_layout()
    plt.show()

sine 파를 생성할 때 주파수로 7 Hz를 사용하였더니 FFT 결과 7 HZ 위치에만 값이 존재합니다.

전체 코드입니다.

# 참고
# https://tuttozurich.tistory.com/15
# https://github.com/hazevt04/fft_sine_wave/blob/main/fft_sine_wave.py

import numpy as np
from matplotlib import pyplot as plt

freq = 7 # Frequency of the Sinewave
rate = 1000 # Sampling Rate
time_interval = 3 # Sampling Interval

t = np.linspace(0, time_interval, time_interval*rate) # Time-Axis
y1 = 2*np.sin(2*np.pi*freq*t) # Sinewave
y2 = 4*np.sin(2*np.pi*freq*t + 2) # Sinewave

def PositiveFFT(x, Fs):
Ts = 1/Fs
Nsamp = x.size
xFreq = np.fft.rfftfreq(Nsamp, Ts)[:-1]
yFFT = (np.fft.rfft(x)/Nsamp)[:-1]*2
return xFreq, yFFT

# Calculate FFT
xFreq1, FFT_data1 = PositiveFFT(y1, rate)
xFreq2, FFT_data2 = PositiveFFT(y2, rate)

# Plot the FFT
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize = (10,5))
ax1.plot(t, y1)
ax1.set_title('signal')
ax1.set_xlabel('time')
ax1.set_ylabel('amplitude')
ax1.set_xlim(0,1)
ax2.stem(xFreq1, abs(FFT_data1), use_line_collection=True)
ax2.grid(True)
ax2.set_title(r"$\frac{2 \cdot fft(s)}{len(s)}$")
ax2.set_xlabel('freq')
ax2.set_ylabel('amplitude')
ax2.set_xlim(0,10)
ax3.plot(t, y2)
ax3.set_title('signal')
ax3.set_xlabel('time')
ax3.set_ylabel('amplitude')
ax3.set_xlim(0,1)
ax4.stem(xFreq2, abs(FFT_data2), use_line_collection=True)
ax4.grid(True)
ax4.set_title(r"$\frac{2 \cdot fft(s)}{len(s)}$")
ax4.set_xlabel('freq')
ax4.set_ylabel('amplitude')
ax4.set_xlim(0,10)
plt.tight_layout()
plt.show()

5 Hz, 7 Hz, 9 Hz 사인파를 더한 후, FFT 변환하여 스펙트럼을 그려보았습니다. 사인파를 위한 주파수별로 성분이 검출되었습니다.

# 참고
# https://tuttozurich.tistory.com/15
# https://github.com/hazevt04/fft_sine_wave/blob/main/fft_sine_wave.py
# https://alice-secreta.tistory.com/22
# https://techreviewtips.blogspot.com/2017/11/05-02-fft.html

import numpy as np
from matplotlib import pyplot as plt

freq1 = 5 # Frequency of the Sinewave 5 Hz
freq2= 7    # 7 Hz
freq3 = 9 # 9 Hz
Fs = 1000     # Sampling Rate
time_interval = 1 # Sampling Interval

t = np.arange(0, time_interval, 1/Fs)

# 5Hz에 진폭이 2인 시그널을 1초동안 샘플링한다.
y1 = 2*np.cos(2*np.pi*freq1*t) # Sinewave
y1 += 2*np.cos(2*np.pi*freq2*t) # Sinewave
y1 += 2*np.cos(2*np.pi*freq3*t) # Sinewave

def PositiveFFT(x, Fs):
    Ts = 1/Fs
    Nsamp = x.size
    xFreq = np.fft.rfftfreq(Nsamp, Ts)[:-1]
    yFFT = (np.fft.rfft(x)/Nsamp)[:-1]*2

    # yFFT = (np.fft.fft(x)/Nsamp)
    # yFFT = np.abs(yFFT[:int(Nsamp/2)])*2# 두배를 해야 하는가?
    # xFreq = np.fft.fftfreq(Nsamp, Ts)[:int(Nsamp/2)]

    return xFreq, yFFT

# Calculate FFT
xFreq1, FFT_data1 = PositiveFFT(y1, Fs)

print(y1.shape, FFT_data1.shape)

# Plot the FFT
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (10,5))
ax1.plot(t, y1)
ax1.set_title('signal')
ax1.set_xlabel('time')
ax1.set_ylabel('amplitude')
ax1.set_xlim(0,1)
ax2.stem(xFreq1, abs(FFT_data1), use_line_collection=True)
ax2.grid(True)
ax2.set_title(r"$\frac{2 \cdot fft(s)}{len(s)}$")
ax2.set_xlabel('freq')
ax2.set_ylabel('amplitude')
ax2.set_xlim(0,10)
plt.tight_layout()
plt.show()

저작자표시 비영리 변경금지